Lertap analyses are defined by placing lines in a worksheet called CCs . Here are some real life examples:
Example 1
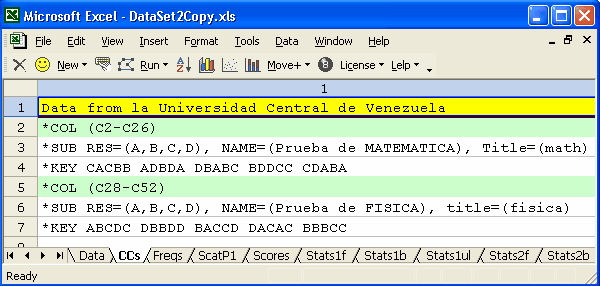
This examples tells Lertap that the responses found in the Data worksheet are grouped into two tests, or subtests. The first group is found in columns 2 through 26; the second in columns 28 through 52. The Res= declaration seen on the *SUB "cards" tell Lertap to recognise only {A,B,C,D} as valid item response codes (this is the default for cognitive items, and generally need not be mentioned). The entries on the *KEY cards indicate what you'd probably expect: the right answers to the items.
This example has two subtests, each effectively defined by a *COL card. In theory, there's no limit to the number of subtests which may be defined; in practice the number is limited by the amount of memory your computer has. To date the greatest number of subtests we've seen has been 22, but there's no reason to think that the number couldn't go much higher. Of interest to some is that any item may appear in any number of subtests, and may be scored differently in each.
Example 2
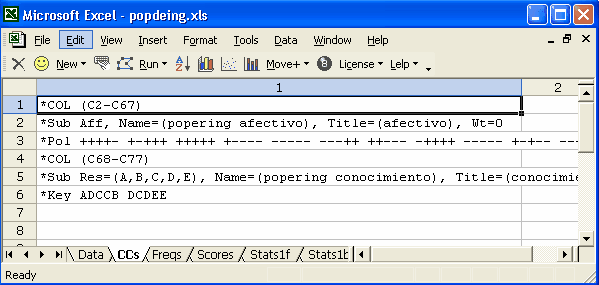
This example, again from Venezuela, also has two subtests. The first is affective -- it involved 66 Likert items which asked first-year engineering students to indicate how they felt about various aspects of their initial year of study. Each Likert item used {1,2,3,4,5} as possible responses. The *Pol "card" tells Lertap that the first four items are to be forward-scored, while the fifth is to be reversed.
The second subtest in this example is a cognitive one. Ten questions were asked in an effort to determine how much the students actually knew about the operation of their school, the university, and the various resources available to assist them. Each of these items use {A,B,C,D,E} as response codes.
The Wt= assignment on the *Sub card controls the weight applied to each subtest when Lertap goes to compute an overall test score, something it generally does by adding weighted subtest scores together. In this example, both subtests had Wt=0, and Lertap did not make a total test score.
Example 3
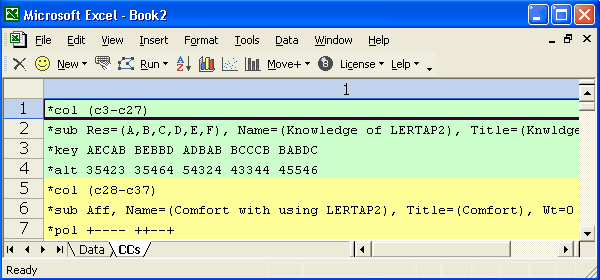
This is another example with two subtests, and again the subtest types are mixed.
The first subtest has 25 cognitive items. The *alt card tells Lertap that the first item uses just the first 3 of the response codes seen in the Res= assignment on the *sub card, that is, {A,B,C}. Only two of this subtest's items used all 6 response codes.
The second subtest is an affective one with 10 items. Four of the items are to be forward-scored; six are reversed.
Example 4
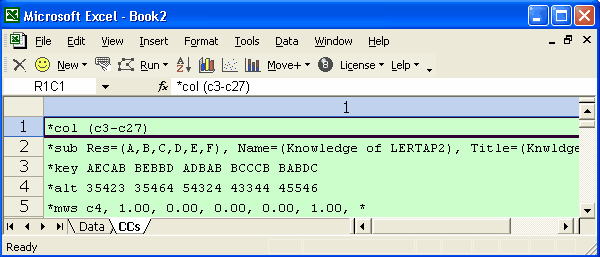
The most powerful "card" which may be used in the CCs worksheet is *mws. MWS stands for multiple-weights specification. Here, the item whose responses reside in c4, column 4 of the Data worksheet, is to be scored so that anyone who takes the first option, which is A, will get 1.00 points. Responses B, C, and D get 0.00 points. Response E gets 1.00 points, and the last response, F, is not used.
This item's scoring had already been defined by the *key and *alt cards; according to *key, the correct answer is E, while *alt says that the item used only the first 5 response codes. The *mws card overrides *key and *alt, and, in this case, double-keys the item found in column 4, defining A and E as correct answers.
Example 5
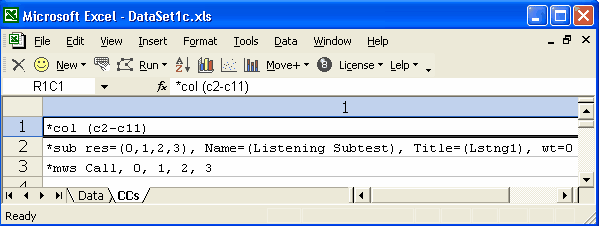
This is an example of how pre-scored items are processed. The res= assignment tells Lertap to recognise {0,1,2,3} as valid entries in columns 2 through 11. The *mws card says that all columns (or ColumnsAll) are to be scored by giving 0 points to the first character found in the res= assignment, 1 point to the second character, and so on. Effectively, *mws Call tells Lertap that the characters found in all columns are to be interpreted as digits, or, if you want, as "points".
Example 6
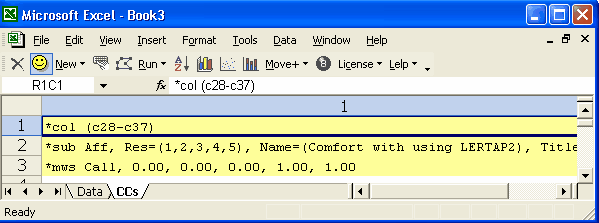
This example takes Likert items and re-scores them so that the first three responses get 0.00 points, while the last two responses get 1.00 points. This type of recoding is sometimes encountered when a user wants to recode Likert items so that they're scored on a dichotomous basis.
Example 7
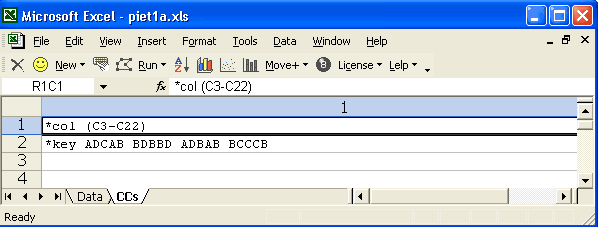
I have provided this example, and the following, to indicate how simple the CCs lines can look. Here a high school chemistry teacher has given his class a 20-item quiz on the atomic table. The teacher was happy with a straightforward Lertap analysis, and knew that these two cards are all that's required to process a cognitive test when all items use {A,B,C,D} as possible responses.
Example 8
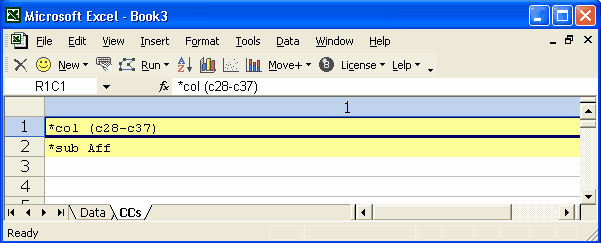
These two CCs cards are all that would be needed to process a 10-item affective instrument, assuming all items used {1,2,3,4,5} as possible responses, and no items were to be reversed.
Example 9
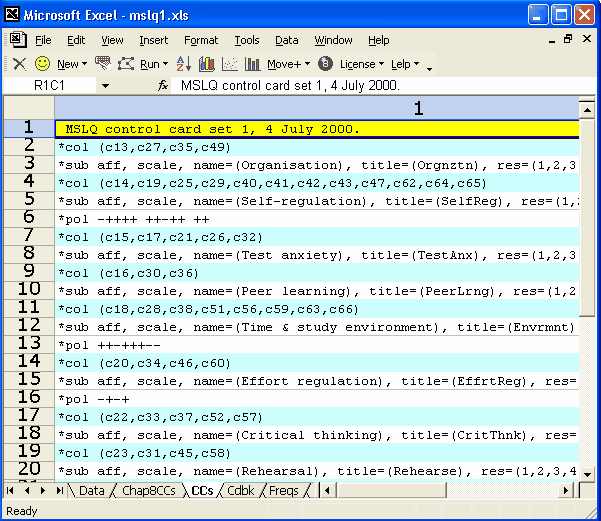
This, the last example of CCs, indicates a job with many affective subtests. How many? Count the *col cards -- there are 8 above. Note how the items in the subtests are generally not found in adjacent columns, and how only some subtests have items in need of reverse scoring (not all subtests make use of a *pol card; if a *pol card is not found, Lertap assumes no items are to be reversed). This example is from a study which used some of the scales in the "MSLQ", Motivated Strategies for Learning Questionnaire, an instrument developed at the University of Michigan.


