Summary statistics

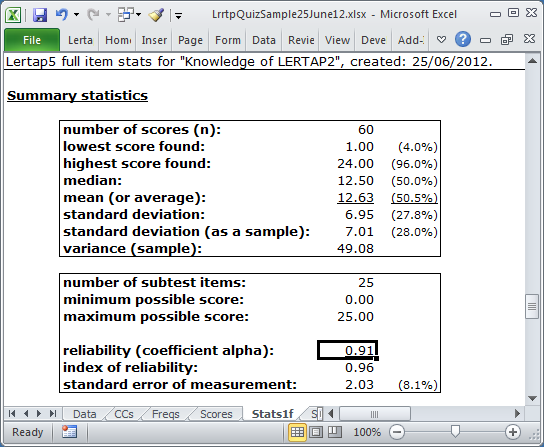
number of scores (n)

This figure corresponds to the number of students whose item responses are found in the Data worksheet. Lertap creates a test score for each student when the Elmillon option is used. The actual test scores are found in the Scores worksheet.

lowest score found

Of all the scores, this figure is the lowest one found. The figure in parentheses, (4%) in this example, expresses the lowest score as a percentage of the maximum possible score. In this example, the maximum possible score was 25.

highest score found

The highest score found. The figure in parentheses, (96%) in this example, expresses this score as a percentage of the maximum possible score.

median

The score which corresponds to the 50th percentile. In this example, half of the scores are below 12.50 and half are above.

mean
(or average)

The average of the test scores, also called the "mean" and the "arithmetic mean". The mean and the median will be equal when the scores are symmetric about the mean.

standard deviation

This is one measure of how spread out the scores are. If all the scores are the same, the standard deviation will be zero. If you are familiar with the equations used to calculate this statistic, Lertap uses the equation with "n" in the denominator to derive this figure.

standard deviation
(as a sample)

If the students tested are considered to be a sample drawn from a larger population, an unbiased estimate of the population standard deviation is given by this figure. If you are familiar with the equations used to calculate the standard deviation, Lertap uses the equation with "n-1" in the denominator to derive this value.

variance (sample)

The square of the standard deviation (sample). Another measure of how spread out the scores are.

number of subtest items

This is the number of items in the test (or subtest).

minimum possible score

Corresponds to the lowest possible score which a student could get on the test. For a cognitive test, this is usually zero, meaning no items correct.

maximum possible score

The highest possible test score. On a cognitive test this is usually equal to the number of test items, with a student getting one point for each item answered correctly.

reliability (coefficient alpha)

Derived by applying Cronbach's method to find coefficient alpha. The maximum possible value is 1.00. A "good" cognitive test might be expected to have a reliability of at least 0.80; a "good" affective scale might be expected to have a reliability of at least 0.70. Note (however), that these "good" values are not always appropriate. A "mastery" test, for example, will sometimes be acceptable even when its reliability, as measured by alpha, is low. Affective scales frequently have alpha reliabilities below 0.70 -- when this happens, results are often interpreted on an item by item basis instead of the overall scale score.
 
Notes: (1) coefficient alpha may take on negative values; when this happens Lertap reports 0.00 as the reliability figure. (2) KR-20, another reliability estimate, is the same as alpha when cognitive test items are all dichotomous -- see "tidbits" below. (3) McDonald's reliability estimate, "omega", will appear at the end of an IStats report (reference).

index of reliability

In "CTT", classical test theory, this is the correlation between observed scores and true scores. It is computed by finding the square root of the reliability estimate.

standard error of measurement

Often abbreviated as "SEM", this is a measure of measurement precision, inversely related to reliability. Very reliable tests will have little measurement error. The SEM is often used to form "confidence intervals". Adding and subtracting one SEM from any test score gives what is often called the "68% confidence interval", a range of scores which, given certain assumptions, captures the true test score with a probability of 0.68. In CTT, SEM is an average figure. A more accurate estimate of measurement error is found by computing the "conditional standard error of measurement", a figure which varies by test score. Lertap's "csem" report provides estimates of measurement error by test score.